機械学習のモデル性能を向上させるためには、データの前処理が非常に重要です。その中でも「特徴量の変換」は欠かせないステップの一つです。今回は、特徴量をLog変換することのメリットと具体的な方法について詳しく解説します。実際のPythonコードや具体例を交えて説明しますので、ぜひ参考にしてください。
目次
特徴量のLog変換とは?
特徴量のLog変換とは、元のデータに対して対数関数を適用し、新しい特徴量を作成する手法です。具体的には、各データポイントに対して自然対数(ln)や常用対数(log10)を計算します。この変換により、データの分布が変わり、機械学習モデルの性能向上につながることがあります。
Log変換のメリット
1. データの正規化
多くの機械学習アルゴリズムは、データが正規分布に近いほど性能が向上します。Log変換を施すことで、右に歪んだ分布のデータを正規分布に近づけることができます。
2. 外れ値の影響軽減
元のデータに大きな外れ値が存在する場合、それがモデルの学習に悪影響を及ぼすことがあります。Log変換は外れ値の影響を抑え、モデルの安定性を高めます。
3. 関係性の線形化
多くの機械学習アルゴリズムは、特徴量とターゲット変数の関係が線形であることを前提としています。Log変換により、非線形な関係を線形に近づけることが可能です。
具体的な例で理解しよう
例えば、不動産価格の予測を行う際、価格データは通常右に歪んでいます。高額な物件が少数存在するため、平均値が大きくなりがちです。この場合、Log変換を行うことでデータの分布を正規に近づけ、モデルの精度を向上させることが期待できます。
元のデータとLog変換後のデータの比較
以下に、架空の不動産価格データを用いて、Log変換前後のヒストグラムを比較してみましょう。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# サンプルデータの生成(不動産価格)
np.random.seed(0)
prices = np.random.exponential(scale=100, size=1000)
# データフレームの作成
df = pd.DataFrame({'Price': prices})
# Log変換
df['Log_Price'] = np.log(df['Price'])
# ヒストグラムの描画
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(df['Price'], bins=50, color='skyblue', edgecolor='black')
plt.title('価格のヒストグラム(変換前)')
plt.xlabel('価格')
plt.ylabel('頻度')
plt.subplot(1, 2, 2)
plt.hist(df['Log_Price'], bins=50, color='salmon', edgecolor='black')
plt.title('価格のヒストグラム(Log変換後)')
plt.xlabel('Log価格')
plt.ylabel('頻度')
plt.tight_layout()
plt.show()
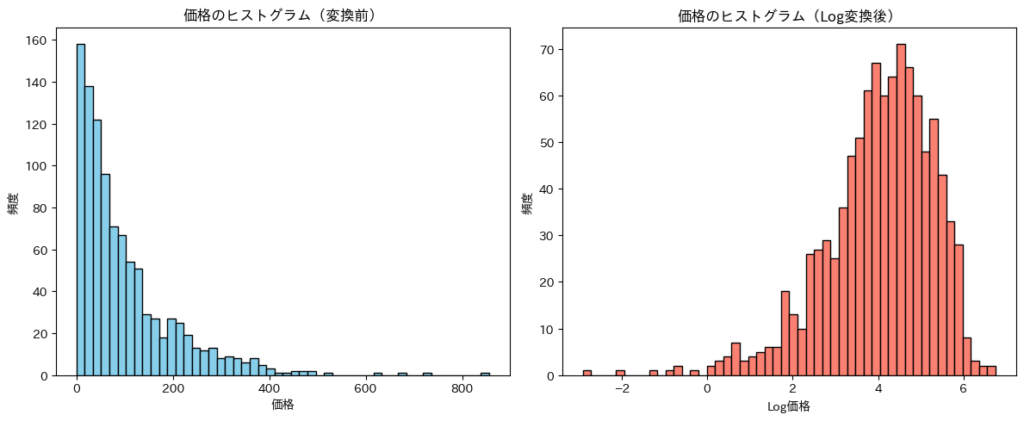
上記のコードでは、指数分布に従う架空の不動産価格データを生成し、Log変換を行っています。ヒストグラムを見ると、変換前は右に大きく歪んでいるのに対し、変換後はより対称的な分布になっていることがわかります。
PythonでのLog変換の実装方法
実際にPythonを使ってLog変換を行う方法を詳しく見ていきましょう。ここでは、Pandasライブラリを使用します。
ステップ1: 必要なライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltステップ2: データの準備
例えば、以下のようなデータフレームがあるとします。
# サンプルデータの生成
data = {
'Feature': [10, 50, 200, 500, 1000, 2000, 5000, 10000]
}
df = pd.DataFrame(data)ステップ3: Log変換の適用
# Log変換(自然対数)
df['Log_Feature'] = np.log(df['Feature'])
# または、常用対数を使用する場合
# df['Log10_Feature'] = np.log10(df['Feature'])
ステップ4: 結果の確認
print(df)出力結果:
Feature Log_Feature
0 10 2.302585
1 50 3.912023
2 200 5.298317
3 500 6.214608
4 1000 6.907755
5 2000 7.600902
6 5000 8.517193
7 10000 9.210340
このように、元の特徴量に対してLog変換を適用することで、新たな特徴量が生成されます。これにより、データの分布がより正規分布に近づき、機械学習モデルの性能が向上する可能性があります。
注意点とベストプラクティス
1. ゼロや負の値に注意
Log変換は、ゼロや負の値に対して定義されていません。そのため、データにゼロや負の値が含まれている場合は、事前に適切な処理を行う必要があります。例えば、最小値をシフトさせる方法があります。
# データにゼロが含まれている場合の処理
df['Feature_Shifted'] = df['Feature'] + 1 # 最小値を1にシフト
df['Log_Feature'] = np.log(df['Feature_Shifted'])
2. モデルに応じた変換の選択
すべてのモデルでLog変換が有効というわけではありません。例えば、ツリーベースのモデル(決定木、ランダムフォレスト、XGBoostなど)は、特徴量の分布にそれほど敏感ではありません。一方、線形回帰やロジスティック回帰などのモデルでは、Log変換が有効な場合があります。
3. 逆変換の必要性
モデルの予測結果を解釈する際、Log変換を行った特徴量を元のスケールに戻す必要がある場合があります。これは、予測結果を実際の値に戻すためです。
# 予測結果の逆変換
predictions_log = model.predict(X_test_log)
predictions = np.exp(predictions_log) # 自然対数を使用した場合
まとめ
特徴量のLog変換は、データの分布を正規化し、外れ値の影響を軽減する有力な手法です。特に、線形モデルを使用する際には、モデルの性能を向上させる効果が期待できます。Pythonを用いた具体的な実装方法や、変換前後のデータの変化を視覚的に確認することで、理解を深めることができます。データ前処理の一環として、ぜひLog変換を試してみてください。
