目次
はじめに
製造業や品質管理、商品開発などの分野では、効率的な実験設計が不可欠です。複数の要因が絡む実験では、すべての組み合わせを試すのは時間とコストの面で現実的ではありません。こうした課題を解決するのが直交表(Orthogonal Array)です。
この記事では、L8直交表について詳しく解説し、Pythonを使った要因効果の可視化と分散分析(ANOVA)を行い、効率的な実験計画と分析方法を紹介します。
L8直交表とは?
直交表の概要
直交表は、複数の要因とその水準(レベル)の組み合わせを効率よく網羅するための実験計画法です。全組み合わせを試さなくても、主要な要因や交互作用の効果を把握できます。
L8直交表の特徴
- 試行回数(行数):8回
- 要因のレベル数:2レベル(例:「多い」「少ない」など)
- 最大要因数:7個(交互作用を含む)
L8直交表の基本構造(7要因)
| 実験回数 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 1 | 1 | 2 | 2 | 2 |
| 4 | 1 | 2 | 2 | 2 | 1 | 1 | 1 |
| 5 | 2 | 1 | 1 | 2 | 1 | 2 | 2 |
| 6 | 2 | 1 | 2 | 1 | 2 | 1 | 1 |
| 7 | 2 | 2 | 1 | 2 | 2 | 1 | 1 |
| 8 | 2 | 2 | 2 | 1 | 1 | 2 | 2 |
実例:最適なパンケーキレシピの開発
実験の目的
「小麦粉」「砂糖」「バター」「牛乳」「卵」「ベーキングパウダー」「焼き時間」の7つの要因を変え、最も美味しいパンケーキのレシピを見つけます。
要因と水準
- A:小麦粉(1: 少ない、2: 多い)
- B:砂糖(1: 少ない、2: 多い)
- C:バター(1: 少ない、2: 多い)
- D:牛乳(1: 少ない、2: 多い)
- E:卵(1: 1個、2: 2個)
- F:ベーキングパウダー(1: 少ない、2: 多い)
- G:焼き時間(1: 短い、2: 長い)
実験結果(仮の評価)
| 実験回数 | A | B | C | D | E | F | G | 味の評価(5段階) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 4 |
| 3 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 5 |
| 4 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 4 |
| 5 | 2 | 1 | 1 | 2 | 1 | 2 | 2 | 3 |
| 6 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 5 |
| 7 | 2 | 2 | 1 | 2 | 2 | 1 | 1 | 4 |
| 8 | 2 | 2 | 2 | 1 | 1 | 2 | 2 | 5 |
PythonでL8直交表の作成と要因効果・分散分析
必要なライブラリ
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smfL8直交表の作成とANOVA分析
# データ作成
data = {
'A': [1, 1, 1, 1, 2, 2, 2, 2],
'B': [1, 1, 2, 2, 1, 1, 2, 2],
'C': [1, 2, 1, 2, 1, 2, 1, 2],
'D': [1, 2, 1, 2, 2, 1, 2, 1],
'E': [1, 2, 2, 1, 1, 2, 2, 1],
'F': [1, 2, 2, 1, 2, 1, 1, 2],
'G': [1, 2, 2, 1, 2, 1, 1, 2],
'評価': [3, 4, 5, 4, 3, 5, 4, 5]
}
df = pd.DataFrame(data)
# 分散分析
model = smf.ols('評価 ~ A + B + C + D + E + F + G', data=df).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table) sum_sq df F PR(>F)
A 0.125 1.0 1.0 0.500000
B 1.125 1.0 9.0 0.204833
C 1.125 1.0 9.0 0.204833
D 1.125 1.0 9.0 0.204833
E 1.125 1.0 9.0 0.204833
F 0.125 1.0 1.0 0.500000
G 0.125 1.0 1.0 0.500000
Residual 0.125 1.0 NaN NaNランダムに作成したデータですので、結果が不自然に偏っていますが、PRが有意水準(通常0.05)より小さい場合は有意差があると判断できます。
要因効果図を作成
要因効果図を作成することで、結果を視覚的に解釈することができます。7つの要因をたったの8回の実験で効果を確認することができました!
# 要因効果図を作成
df_melt = df.melt(id_vars='評価', value_name='水準', var_name='要因')
sns.catplot(x='水準', y='評価', data=df_melt, col='要因' ,kind='point', col_wrap=4)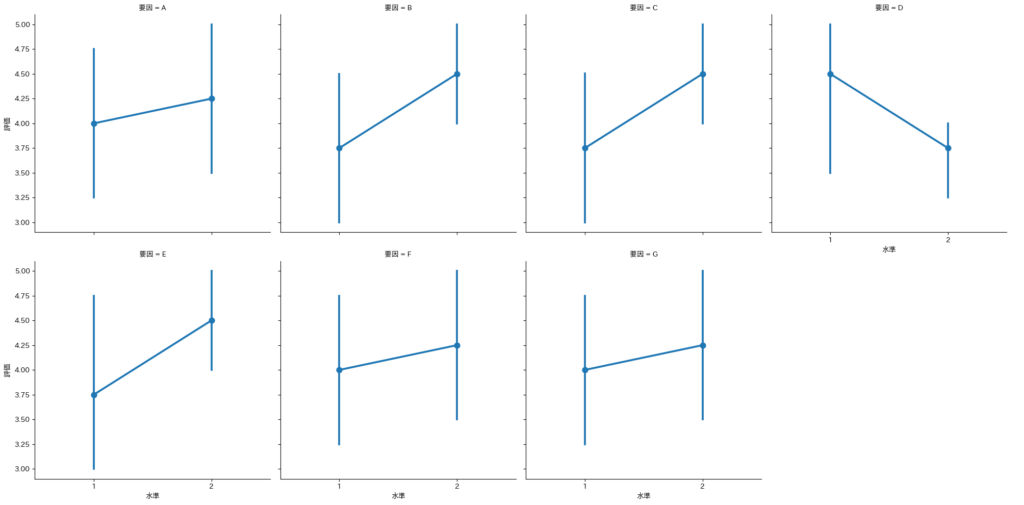
L8直交表における注意点
今回の例では、L8直交表に割り付けられる最大数である7つの要因を割り付けました。しかし、要因間に交互作用がある場合、結果の解釈が変わってきます。次回は、交互作用について解説したいと思います。
まとめ
L8直交表は、効率的な実験設計と要因分析に非常に有効です。Pythonを使うことで、簡単に実験設計・結果分析が可能になります。
