機械学習の特徴量エンジニアリングでは、角度や周期的なデータ(時間、曜日、方位など)を扱う際にsin, cos変換がよく用いられます。この変換を行うことで、周期的なデータの連続性や関係性をより適切にモデルに学習させることができます。
本記事では、sin, cos変換の理論的な背景と、その具体的な応用例を解説します。
目次
なぜsin, cos変換が必要なのか?
周期的なデータ(時間、方角、月日など)は、通常0から360度(または0から1)の範囲で表現されます。しかし、これをそのまま数値特徴量として扱うと、
- 周期性を考慮できない
- 連続性が失われる(例えば、23時と0時の距離が遠いと認識されてしまう)
といった問題が発生します。
例:時間データ(0〜23時)の問題
例えば、時間を0から23の整数値として扱うと、次のような問題が発生します。
| 時間 (hour) | 0 | 1 | 2 | … | 22 | 23 |
|---|---|---|---|---|---|---|
| 数値特徴量 | 0 | 1 | 2 | … | 22 | 23 |
このとき、23と0の距離は23として扱われてしまいますが、本来は隣接しているデータです。この問題を解決するためにsin, cos変換を用います。
sin, cos変換の仕組み
周期的なデータを角度として扱い、sin関数とcos関数を用いて二次元ベクトルに変換する方法です。
変換式:
$$
X_{sin} = \sin\left(\frac{2\pi X}{T}\right)
$$
$$
X_{cos} = \cos\left(\frac{2\pi X}{T}\right)
$$
\(X\) は元の周期的な数値データ(例:時間、角度)
\(T\) は周期(例:24時間、360度)
\(X_{sin}\) と \(X_{cos}\) はそれぞれsin, cos変換後の値
これにより、値の連続性が保たれ、機械学習モデルが周期性を正しく学習できるようになります。
例:時間データ(0〜23時)の変換
| 時間 (hour) | sin変換 | cos変換 |
|---|---|---|
| 0 | 0.0 | 1.0 |
| 6 | 1.0 | 0.0 |
| 12 | 0.0 | -1.0 |
| 18 | -1.0 | 0.0 |
| 23 | -0.2588 | 0.9659 |
0時と23時が隣接した値を持つことが分かります。
sin, cos変換の応用例
1. 時間・曜日データの特徴量変換
機械学習モデルで時系列データや曜日データを扱う際に有効です。
例:曜日データ(0=月曜, 6=日曜)
$$
X_{sin} = \sin\left(\frac{2\pi X}{7}\right),\quad X_{cos} = \cos\left(\frac{2\pi X}{7}\right)
$$
これにより、月曜日(0)と日曜日(6)が適切に隣接した特徴量として扱われます。
2. GPSや方角データの変換
方位データ(0〜360度)をそのままモデルに入力すると、360度と0度が大きく離れた数値として扱われてしまいます。これをsin, cos変換で補正します。
$$
X_{sin} = \sin\left(\frac{2\pi X}{360}\right), \quad X_{cos} = \cos\left(\frac{2\pi X}{360}\right)
$$
これにより、北(0度)と北西(315度)が適切に隣接したデータとして学習されます。
3. 気象データの季節変換
1年の季節(春夏秋冬)も周期的なデータなので、sin, cos変換を適用できます。
$$
X_{sin} = \sin\left(\frac{2\pi X}{365}\right), \quad X_{cos} = \cos\left(\frac{2\pi X}{365}\right)$$
Pythonでの実装例
以下に、時間データをsin, cos変換するPythonコードを示します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 0〜23時のデータを作成
hours = np.arange(0, 24)
T = 24 # 24時間周期
# sin, cos変換
hours_sin = np.sin(2 * np.pi * hours / T)
hours_cos = np.cos(2 * np.pi * hours / T)
# データフレーム化
df = pd.DataFrame({
'hour': hours,
'hour_sin': hours_sin,
'hour_cos': hours_cos
})
# 結果を表示
print(df)
# グラフ表示
plt.figure(figsize=(8, 4))
plt.plot(hours, hours_sin, label='sin')
plt.plot(hours, hours_cos, label='cos')
plt.xlabel('Hour')
plt.ylabel('Value')
plt.legend()
plt.title('Sin-Cos Transformation of Hour Data')
plt.grid()
plt.show()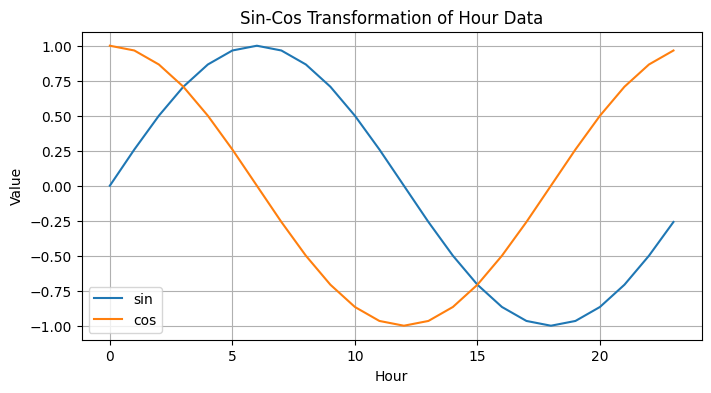
このコードを実行すると、時間データがsin, cos変換され、グラフで視覚的に確認できます。
まとめ
- sin, cos変換は周期的データの連続性を保つために重要
- 時間、方位、季節などのデータで活用可能
- Pythonを使えば簡単に実装できる
機械学習においてsin, cos変換を適切に活用することで、モデルの精度向上につながる可能性があります。ぜひ試してみてください。
